20211103|数海钓鱼每日一题
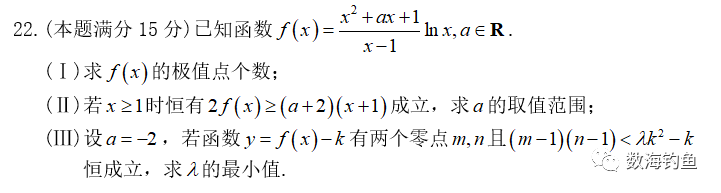
$22. (本题满分15分)已知函数f(x)=\frac{x^{2}+ax+1}{x-1}\ln{x}, a\in{\mathbb{R}}. $
$(I)求f(x)的极值点个数; $
$(II)若x\geq 1时恒有2f(x)\geq (a+2)(x+1)成立, 求a的取值范围; $
$(III)设a=-2, 若函数y=f(x)-k有两个零点m, n且(m-1)(n-1)<\lambda k^{2}-k恒成立, 求\lambda 的最小值. $
(I)(II) 没导明白
(III)
重量寄的来了, 说实话确实没导明白这题, 如果放考场上2个小时全做这题也大概率被创飞
先换元
$x_{1}=\ln{m}, x_{2}=\ln{n}, x_{1}<x_{2}, h_{1}(x)=x(e^{x}-1), h_{1}(x_{1})=h_{1}(x_{2})=k$
构造函数
$h_{2}(x)=\lambda (x^{2}e^{x}-x^{2})-((\frac{1}{2}x-1)e^{x}+\frac{1}{2}x+1)$
求导
$h_2’(x)=\lambda ((x^{2}+2x)e^{x}-2x)-\frac{1}{2}((x-1)e^{x}+1)$
$h_{2}’’(x)=\lambda ((x^{2}+4x+2)e^{x}-2)-\frac{1}{2}xe^{x}$
$h_{2}’’’(x)=\lambda (x^{2}+6x+6)e^{x}-\frac{1}{2}(x+1)e^{x}$
先证$\lambda <\frac{1}{12}$时不成立
若$\lambda <\frac{1}{12}$
则$h_{2}’’’(0)=6\lambda -\frac{1}{2}<0$
又$h_{2}’’’(x)$为$\mathbb{R}$上连续函数
故存在包含$0$的一个连续开区间$U_{1}$
满足$\forall x\in{U_{1}}$均有$h_{2}’’’(x)<0$
即$h_{2}’’’(x)$在$U_{1}$上恒小于$0$
$h_{2}’’(x)$在$U_{1}$上单调递减
$x\in{(-\infty, 0)\cap U_{1}}$, $h_{2}’’(x)>h_{2}’’(0)=0$, $h_{2}’(x)$单调递增, $h_{2}’(x)<h_2’(0)=0$, $h_{2}$单调递减;
$x\in{U_{1}\cap (0, +\infty)}$, $h_{2}’’(x)<h_{2}’’(0)=0$, $h_{2}’(x)$单调递减, $h_{2}’(x)<h_2’(0)=0$, $h_{2}$单调递减;
因此$h_{2}(x)$在$U_{1}$上单调递减
又$k\to 0^{+}$时$x_{1}\to 0^{-}$, $x_{2}\to 0^{+}$
故存在$k$使得$x_{1}\in{U_{1}}$, $x_{2}\in{U_{1}}$
$x_{1}<x_{2}$
$\Leftrightarrow h_{2}(x_{1})>h_{2}(x_{2})$
$\Leftrightarrow \lambda ({x_{1}}^{2}e^{x_{1}}-{x_{1}}^{2})-((\frac{1}{2}x-1)e^{x_{1}}+\frac{1}{2}x_{1}+1)>\lambda ({x_{2}}^{2}e^{x}-{x_{2}}^{2})-((\frac{1}{2}x_{2}-1)e^{x_{2}}+\frac{1}{2}x_{2}+1)$
$\Leftrightarrow \lambda {x_{1}}^{2}(e^{x_{1}}-1)-(\frac{1}{2}x_{1}(e^{x_{1}}-1)-e^{x_{1}}+x_{1}+1)>\lambda {x_{2}}^{2}(e^{x_{2}}-1)-(\frac{1}{2}x_{2}(e^{x_{2}}-1)-e^{x_{2}}+x_{2}+1)$
$\Leftrightarrow \lambda x_{1}k-x_{1}-\frac{1}{2}k+(e^{x_{1}}-1)>\lambda x_{2}k-x_{2}-\frac{1}{2}k+(e^{x_{2}}-1)$
$\Leftrightarrow \frac{x_{1}}{k}(\lambda k^{2}-k)+\frac{x_{2}}{k}(e^{x_{1}}-1)(e^{x_{2}}-1)>\frac{x_{2}}{k}(\lambda k^{2}-k)+\frac{x_{1}}{k}(e^{x_{1}}-1)(e^{x_{2}}-1)$
$\Leftrightarrow \frac{x_{2}}{k}(e^{x_{1}}-1)(e^{x_{2}}-1)-\frac{x_{1}}{k}(e^{x_{1}}-1)(e^{x_{2}}-1)>\frac{x_{2}}{k}(\lambda k^{2}-k)-\frac{x_{1}}{k}(\lambda k^{2}-k)$
$\Leftrightarrow (\frac{x_{2}}{k}-\frac{x_{1}}{k})(e^{x_{1}}-1)(e^{x_{2}}-1)>(\frac{x_{2}}{k}-\frac{x_{1}}{k})(\lambda k^{2}-k)$
$\Leftrightarrow (e^{x_{1}}-1)(e^{x_{2}}-1)>\lambda k^{2}-k$
与$(m-1)(n-1)<\lambda k^{2}-k恒成立$即$(e^{x_{1}}-1)(e^{x_{2}}-1)<\lambda k^{2}-k恒成立$矛盾
故$\lambda \geq \frac{1}{12}$
再证$\lambda = \frac{1}{12}$时$(e^{x_{1}}-1)(e^{x_{2}}-1)<\lambda k^{2}-k恒成立$
若$\lambda = \frac{1}{12}$
$h_{2}’’’(x)=\frac{1}{12}x^{2}e^{x}\geq 0$, 当且仅当$x=0$时取等
$h_{2}’’(x)$单调递增
$x\in{(-\infty, 0)}$时, $h_{2}’’(x)<h_{2}’’(0)=0$,$h_{2}’(x)$单调递减, $h_{2}’(x)>h_2’(0)=0$, $h_{2}(x)$单调递增;
$x\in{(0, +\infty)}$时, $h_{2}’’(x)>h_{2}’’(0)=0$,$h_{2}’(x)$单调递增, $h_{2}’(x)>h_2’(0)=0$, $h_{2}(x)$单调递增;
故$h_{2}(x)$在$\mathbb{R}$上单调递增
$x_{1}<x_{2}$
$\Leftrightarrow h_{2}(x_{1})<h_{2}(x_{2})$
$\Leftrightarrow \lambda ({x_{1}}^{2}e^{x_{1}}-{x_{1}}^{2})-((\frac{1}{2}x-1)e^{x_{1}}+\frac{1}{2}x_{1}+1)<\lambda ({x_{2}}^{2}e^{x}-{x_{2}}^{2})-((\frac{1}{2}x_{2}-1)e^{x_{2}}+\frac{1}{2}x_{2}+1)$
$\Leftrightarrow \lambda {x_{1}}^{2}(e^{x_{1}}-1)-(\frac{1}{2}x_{1}(e^{x_{1}}-1)-e^{x_{1}}+x_{1}+1)<\lambda {x_{2}}^{2}(e^{x_{2}}-1)-(\frac{1}{2}x_{2}(e^{x_{2}}-1)-e^{x_{2}}+x_{2}+1)$
$\Leftrightarrow \lambda x_{1}k-x_{1}-\frac{1}{2}k+(e^{x_{1}}-1)<\lambda x_{2}k-x_{2}-\frac{1}{2}k+(e^{x_{2}}-1)$
$\Leftrightarrow \frac{x_{1}}{k}(\lambda k^{2}-k)+\frac{x_{2}}{k}(e^{x_{1}}-1)(e^{x_{2}}-1)<\frac{x_{2}}{k}(\lambda k^{2}-k)+\frac{x_{1}}{k}(e^{x_{1}}-1)(e^{x_{2}}-1)$
$\Leftrightarrow \frac{x_{2}}{k}(e^{x_{1}}-1)(e^{x_{2}}-1)-\frac{x_{1}}{k}(e^{x_{1}}-1)(e^{x_{2}}-1)<\frac{x_{2}}{k}(\lambda k^{2}-k)-\frac{x_{1}}{k}(\lambda k^{2}-k)$
$\Leftrightarrow (\frac{x_{2}}{k}-\frac{x_{1}}{k})(e^{x_{1}}-1)(e^{x_{2}}-1)<(\frac{x_{2}}{k}-\frac{x_{1}}{k})(\lambda k^{2}-k)$
$\Leftrightarrow (e^{x_{1}}-1)(e^{x_{2}}-1)<\lambda k^{2}-k$
即$\lambda$最小值为$\frac{1}{12}$
现在我们来处理两个问题, 一小一大
先看小问题
$h_{2}(x)$是如何构造xjb凑出来的
回到$(e^{x_{1}}-1)(e^{x_{2}}-1)<\lambda k^{2}-k$
同乘$(\frac{x_{2}}{k}-\frac{x_{1}}{k})$即$(\frac{1}{e^{x_{2}}-1}-\frac{1}{e^{x_{1}}-1})$制造同构式
得到$\lambda {x_{1}}^{2}(e^{x_{1}}-1)-x_{1}+(e^{x_{1}}-1)<\lambda {x_{2}}^{2}(e^{x_{2}}-1)-x_{2}+(e^{x_{2}}-1)$
令$h_{3}(x)=\lambda x^{2}(e^{x}-1)-x+(e^{x}-1)$
但是我们发现$h_{3}(x)$不是一个$\mathbb{R}$上的单调递增函数, 与我们期望的不同
那怎么办?
这部分思想有点类似拉格朗日乘数法, 直线系, 曲线系之类的
如果我们构造两个函数$h_{4}(x, y)$, $h_{5}(x)=h_{4}(h_{3}(x), h_{1}(x))$均是关于$x$单调递增的
那么有$h_{5}(x_{1})=h_{4}(h_{3}(x_{1}), h_{1}(x_{1}))<h_{5}(x_{2})=h_{4}(h_{3}(x_{2}), h_{1}(x_{2}))$
不就有$h_{3}(x_{1})<h_{3}(x_{2})$了吗?
实际上一般构造的是$h_{4}(x, y)=x+\mu y$
本题中是依据$\lambda \geq \frac{1}{12}$取的$\mu =-\frac{1}{2}$
具体细节不详细描述, 可参看
现在来看大问题
$\frac{1}{12}$是怎么来的
前置知识: 洛必达法则, 隐函数求导
$(e^{x_{1}}-1)(e^{x_{2}}-1)<\lambda k^{2}-k$
$\Leftrightarrow \frac{(e^{x_{1}}-1)(e^{x_{2}}-1)}{k^{2}}<\frac{\lambda k^{2}-k}{k^{2}}$
$\Leftrightarrow \frac{1}{x_{1}x_{2}}+\frac{1}{k}<\lambda$
$h_{6}(k)=\frac{1}{x_{1}x_{2}}+\frac{1}{k}$
一个直觉是$k\to 0^{+}$时$h_{6}(k)$最大(我也不知道为什么这是对的)
$\lim_{k\to 0^{+}}h_{6}(k)$怎么求?
$h_{7}(x)=\sqrt{h_{1}(x)}=\sqrt{x(e^{x}-1)}$
取根号的原因自己算算就知道, 后面极限最起码不是$0$或$\infty$你就偷着乐吧
$h_{7}’(x)=\frac{(x+1)e^{x}-1}{2 \sqrt{x(e^{x}-1)}}$
$h_{7}’’(x)=\frac{(x^{2}+2x-1)e^{2x}-2(x^{2}+x-1)e^{x}-1}{4(x(e^{x}-1))^{3/2}}$
$h_{7}’’’(x)=\frac{(x^{3}+3x^{2}-3x+3)e^{3x}-(2x^{3}+9x^{2}-6x+9)e^{2x}+(4x^{3}+6x^{2}-3x+9)e^{x} -3}{8(x(e^{x}-1))^{5/2}}$
$h_{7}’’’’(x)=\frac{((x^{4}+4x^{3}-6x^{2}+12x-15)e^{4x}-4(x^{4}+3x^{3}-6x^{2}+9x-15)e^{3x}-(4x^{4}-24x^{3}+30x^{2}-36x+90)e^{2x}-4(2x^{4}+4x^{3}-3x^{2}+3x-15)e^{x}-15)}{16(x(e^{x}-1))^{7/2}}$
$h_{7}(x_{1})=\sqrt{h_{1}(x_{1})}=\sqrt{x_{1}(e^{x_{1}}-1)}=\sqrt{k}=t$
$h_{7}(x_{2})=\sqrt{h_{1}(x_{2})}=\sqrt{x_{2}(e^{x_{2}}-1)}=\sqrt{k}=t$
$h_{8}(t)=\frac{1}{x_{1}x_{2}}+\frac{1}{t^{2}}$
$h_{9}(t)=x_1$
$h_{10}(t)=x_2$
则
$h_{7}(h_{9}(t))=t$
$h_{7}(h_{10}(t))=t$
对$t$求导得
$h_{9}’(t)h_{7}’(h_{9}(t))=1$
$h_{10}’(t)h_{7}’(h_{10}(t))=1$
即
$h_{9}’(t)h_{7}’(x_{1})=1$
$h_{10}’(t)h_{7}’(x_{2})=1$
可得
$h_{9}’(t)=\frac{1}{h_{7}’(x_{1})}$
$h_{10}’(t)=\frac{1}{h_{7}’(x_{2})}$
重复对$t$求导可得
$h_{9}’’(t)=-\frac{h_{7}’’(x_{1})}{(h_{7}’(x_{1}))^{3}}$
$h_{10}’’(t)=-\frac{h_{7}’’(x_{2})}{(h_{7}’(x_{2}))^{3}}$
$h_{9}’’’(t)=\frac{3(h_{7}’’(x_{1}))^{2}-h_{7}’’’(x_{1})h_{7}’(x_{1})}{(h_{7}’(x_{1}))^{5}}$
$h_{10}’’’(t)=\frac{3(h_{7}’’(x_{2}))^{2}-h_{7}’’’(x_{2})h_{7}’(x_{2})}{(h_{7}’(x_{2}))^{5}}$
$h_{9}’’’’(t)=\frac{10h_{7}’’’(x_{1})h_{7}’’(x_{1})h_{7}’(x_{1})-h_{7}’’’’(x_{1})(h_{7}’(x_{1}))^{2}-15(h_{7}’’(x_{1}))^{3}}{(h_{7}’(x_{1}))^{7}}$
$h_{10}’’’’(t)=\frac{10h_{7}’’’(x_{2})h_{7}’’(x_{2})h_{7}’(x_{2})-h_{7}’’’’(x_{2})(h_{7}’(x_{2}))^{2}-15(h_{7}’’(x_{2}))^{3}}{(h_{7}’(x_{2}))^{7}}$
$h_{11}(t)=h_{9}(t)h_{10}(t)$
$h_{11}’(t)=h_{9}’(t)h_{10}(t)+h_{9}(t)h_{10}’(t)$
$h_{11}’’(t)=h_{9}’’(t)h_{10}(t)+2h_{9}’(t)h_{10}’(t)+h_{9}(t)h_{10}’’(t)$
$h_{11}’’’(t)=h_{9}’’’(t)h_{10}(t)+3h_{9}’’(t)h_{10}’(t)+3h_{9}’(t)h_{10}’’(t)+h_{9}(t)h_{10}’’’(t)$
$h_{11}’’’’(t)=h_{9}’’’’(t)h_{10}(t)+4h_{9}’’’(t)h_{10}’(t)+6h_{9}’’(t)h_{10}’’(t)+4h_{9}’(t)h_{10}’’’(t)+h_{9}(t)h_{10}’’’’(t)$
$\lim_{x\to 0^{-}}h_{7}’(x)=-1$
$\lim_{x\to 0^{+}}h_{7}’(x)=1$
$\lim_{x\to 0^{-}}h_{7}’’(x)=-\frac{1}{2}$
$\lim_{x\to 0^{+}}h_{7}’’(x)=\frac{1}{2}$
$\lim_{x\to 0^{-}}h_{7}’’’(x)=-\frac{5}{16}$
$\lim_{x\to 0^{+}}h_{7}’’’(x)=\frac{5}{16}$
$\lim_{x\to 0^{-}}h_{7}’’’’(x)=-\frac{3}{16}$
$\lim_{x\to 0^{+}}h_{7}’’’’(x)=\frac{3}{16}$
$\lim_{t\to 0^{+}}h_{9}(t)=0$
$\lim_{t\to 0^{+}}h_{10}(t)=0$
$\lim_{t\to 0^{+}}h_{9}’(t)=-1$
$\lim_{t\to 0^{+}}h_{10}’(t)=1$
$\lim_{t\to 0^{+}}h_{9}’’(t)=-\frac{1}{2}$
$\lim_{t\to 0^{+}}h_{10}’’(t)=-\frac{1}{2}$
$\lim_{t\to 0^{+}}h_{9}’’’(t)=-\frac{7}{16}$
$\lim_{t\to 0^{+}}h_{10}’’’(t)=\frac{7}{16}$
$\lim_{t\to 0^{+}}h_{9}’’’’(t)=-\frac{1}{2}$
$\lim_{t\to 0^{+}}h_{10}’’’’(t)=-\frac{1}{2}$
$\lim_{t\to 0^{+}}h_{11}(t)=0$
$\lim_{t\to 0^{+}}h_{11}’(t)=0$
$\lim_{t\to 0^{+}}h_{11}’’(t)=-2$
$\lim_{t\to 0^{+}}h_{11}’’’(t)=0$
$\lim_{t\to 0^{+}}h_{11}’’’’(t)=-2$
$\lim_{t\to 0^{+}}h_{8}(t)=\frac{1}{h_{11}(t)}+\frac{1}{t^{2}}=\frac{t^{2}+h_{11}(t)}{h_{11}(t)t^{2}}=\frac{2t+h_{11}’(t)}{h_{11}(t)t^{2}+2h_{11}(t)t}=\frac{h_{11}’’(t)+2}{4h_{11}’(t)t+h_{11}’’(t)t^{2}+2h_{11}(t)}=\frac{h_{11}’’’(t)}{6h_{11}’’(t)t+6h_{11}’(t)+h_{11}’’’(t)t^{2}}=\frac{h_{11}’’’’(t)}{12h_{11}’’(t)+8h_{11}’’’(t)t+h_{11}’’’’(t)t^{2}}=\frac{-2}{-24}=\frac{1}{12}$
$Q.E.D$
